Bilgisayar mühendisliği ya da bilgisayar bilimleri’nin önemli derslerinden olan veri yapılarında işlenen bu arama algoritmasını anlatacağım. Genel olarak verilen bir dizi üzerinde ikiye bölerek aradığımız elemanı bulmamıza yarayan algoritmadır. Bu anlatımda ikili arama(binary search) diziler üzerinden anlatıcaktır. Bu algoritma dizi dışında bir çok farklı veri alanlarında kullanılabilir.
İkili arama(binary search) algoritmasının özellikleri:
- Parçala ve fethet(divide and conquere) yöntemiyle çalışır.
- T(n) hesabı,O(log n)‘dir.
- Dizi sıralı olmalıdır.
İkili arama(binary search) algoritmasının çalışma mantığı
-
Dizinin indis bakımından ortadaki elemanını bulunur.
-
Eğer aranan eleman ortadaki elemana eşit ise aramayı sonlandır.
-
Eğer ortadaki elemana eşit değilse ve ortadaki elemandan büyükse ortadaki elamanın sağ tarafına(büyük elemanlarına) bak.
-
Eğer ortadaki elemana eşit değilse ve ortadaki elemandan küçükse ortadaki elamanın sol tarafına(küçük elemanlarına) bak.
-
Eğer aramadaki bakılan aralık 1 veya daha düşükse aranan eleman bulunamamıştır.
Bu algoritmik adımların her birinde diziyi her zaman ikiye böler. Yani problem log2(n) adımda çözülmesi beklenir. Daha iyi anlaşılması için bir dizi üzerinden örnekle açıklayalım.
Örnek:
int DiziOrnek[8]={1,4,9,10,22,30,35,43,45}; Aranan Sayı:10
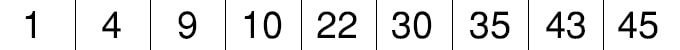
Dizimizin uzunluğu 9 olduğundan ortadaki eleman 4.indiste bulunan ’22’ olacaktır. Burada dikkat etmemiz gereken yer ise dizimizin ilk elemanın indisinin 0 olduğunu bilmemiz gerek.

Birinci adım:
22 eşit midir 10’a. Değildir.
İkinci adım:
10 küçük müdür 22’den. Evet bu yüzden 22’in solundaki(küçük olan) sayıların ortasındaki değere yani 4’e bakacağız.
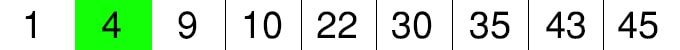
Ortadaki elemanı bulma işlemini yaparken 1 sayısı 0.indis, 10 sayısı 3.indis olduğu için 3/2=1.5 olur.Burada bölüm sonucu ondalıklı bir sayı çıktı bu sayıyı tabana yuvarlama işlemi yapıyoruz yani 1 olarak alıyoruz. Aslında eleman sayısına bakarak bulmakta mümkün. Elemanın sayımız sol taraftaki dizi için 4/2=2 olduğu için dizinin 2.elemanı yani indis olarak 1 olan elemanı almış oluyoruz.
İkinci adımdan sonra tekrarlı bir şekilde birinci ve ikinci adımdaki işlemleri yapmamız gerekecek.
4,10’a eşit değildir ve 10’dan küçüktür. Bu yüzden sağ tarafa(büyük olan) sayılara bakacağız.
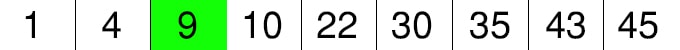
4’ün sağındaki dizide(9 ve 10) ortadaki eleman 9 sayısıdır. 10’a eşit değildir. Bu yüzden sağ tarafa geçerek dizin tek elemanı kaldığı için ortadaki eleman otomatik olarak o sayı olacaktır. 10 sayısının da eşit olup olmadığına baktıktan sonra bulup sonlandıracaktır.
İkili arama(binary search) algoritmasının performansı
ikili arama algoritması (binary search algorithm) daha öncede belirttiğim gibi arama yapılan yapıyı sürekli ikiye bölme işlemine tâbi tuttuğu için T(n) hesabı,O(log n)‘dir. En iyi ihtimali ise ilk bölme işlemi sırasında baktığı durumda aradığı değerin bu değere eşit olması,en iyi ihtimalidir. Yine daha önceden belirttiğim gibi ikili arama algoritması(binary search algorithm) sıralı bir yapı üzerinde uygulanır. Eğer sıralı olmayan bir yapı(dizi) üzerinde yapılacaksa öncelikle sıralanması gerekir. En iyi sıralama algoritmalarından olan birleştirme sıralaması(merge sort algorithm) veya hızlı sıralama algoritması(quick sort algorithm) ile O(nlog2(n)) adımda yapılır. Sıralama yaptıktan sonra ikili arama yapılır yani T(n) hesabımız şu şekilde olacaktır:
= nlog2(n) + log2(n) (log2(n) parantezine alırsak) = log2(n) (n+1) işlem ile yapılır.
Doğrusal arama algoritması(linear search algorithm),sıralı yapılar(diziler) için oldukça kötü bir performansa sahiptir.Fakat sıralı olaman dizilir için O(n) performansı ile ikili arama(binary search) algoritmasından daha iyi bir performans verebilir. Sonuç olarak karışık yani sıralı olmayan bir dizi üzerinde arama işlemi yapılacaksa,doğrusal arama algoritması(linear search algorithm) en hızlı ve basit bir algoritmadır.