Bir graph(şekil) üzerinde,belirli bir başlangıç düğümünden diğer tüm düğümlere en kısa yolu bulmamızı sağlayan bir algoritmadır. En kısa yol bulma(shortest path algorithm) algoritmalarından biridir.Bu algoritmada tıpkı dijkstra algoritmasında olduğu gibi ağırlıklı graf üzerinden çalışır.
Algoritmanın çalışma mantığı:
-
Bütün düğümlere sonsuz değeri atanır.
-
Belli bir düğüm seçilir(şart değil).
-
Düğümler arası bulunan her kenar için düğümün o andaki değerinden daha küçük bir değer bulunduysa güncellemesi gerekir.
Bu pseudo kodda,kenar ve düğüm sayısı kadar çalışır. Dijkstra algoritmasını anlatırken eksi(-) değer taşıyan kenarlar üzerinde sağlıklı bir şekilde çalışmaz demiştik.Bunun için bellman ford algoritmasını önermiştik. Şimdi bu iki algoritmanın kırılma noktasını biraz açalım.
Her düğüm güncelleneceği zaman hangi düğümden güncelleme değeri geldi ise onun bilgisi tutmaktadır. Bunun için eksi(-) değer taşıyan kenarlarda bu algoritma sağlıklı bir şekilde çalışır. Dijkstra algoritmasında ise döngüye tekrar girilme ihtimali vardır.
Algoritmanın çalışması:
Graph üzerindeki her düğümü sonsuz değeri atanır.
Bir başlangıç düğümü seçilir.
Graph üzerindeki her kenar,sırası fark etmeksizin alt alta yazılır.
Not:Bu işlem algoritmanın çalışmasını kolaylaştırmak içindir sıralamanın etkileyeceği durum sadece hızdır.Yoksa yapılan iş aynıdır.
Yazılan kenarlar teker teker gidilir.
Eğer güncelleme gerektirecek bir düğüm varsa güncellenir yoksa algoritma sonlanana kadar devam edilir.
Buraya kadar olan kısım algoritmanın pozitif(+) değer taşıyan kenarları içinde eğer(-) değer taşıyan bir kenar varsa durum şöyle devam eder.
Yukarıda bahsettiğim gibi graf üzerinde düğüme gelen güncellemenin hangi düğüm üzerinden geldiğinin üzerine yazılması lazım(eksi değerler için). Yani eksi bir değer içeren kenar varsa yapılan minimum değerlerin yanına hangi düğüden gelindiğinin bilgisinide üzerine yazmamız gerek çünkü burada pozitif(+) değerler taşıyandan farklı olarak eksi(-) değer kenarın gittiği düğüm algotitma bittiğinde geldiği düğüme yani bir geldiği düğümü kaydettiği için ve eksi(-) değer taşıyan kenar için daha az(minimum) değer bulduğu için geriye doğru tekrar çalışır. Dikkat edilecek husus eksi(-) kenar taşıyandan sonra gelen düğüm için güncelleme gerekmez.
Bir örnek üzerinde açıklayalım.
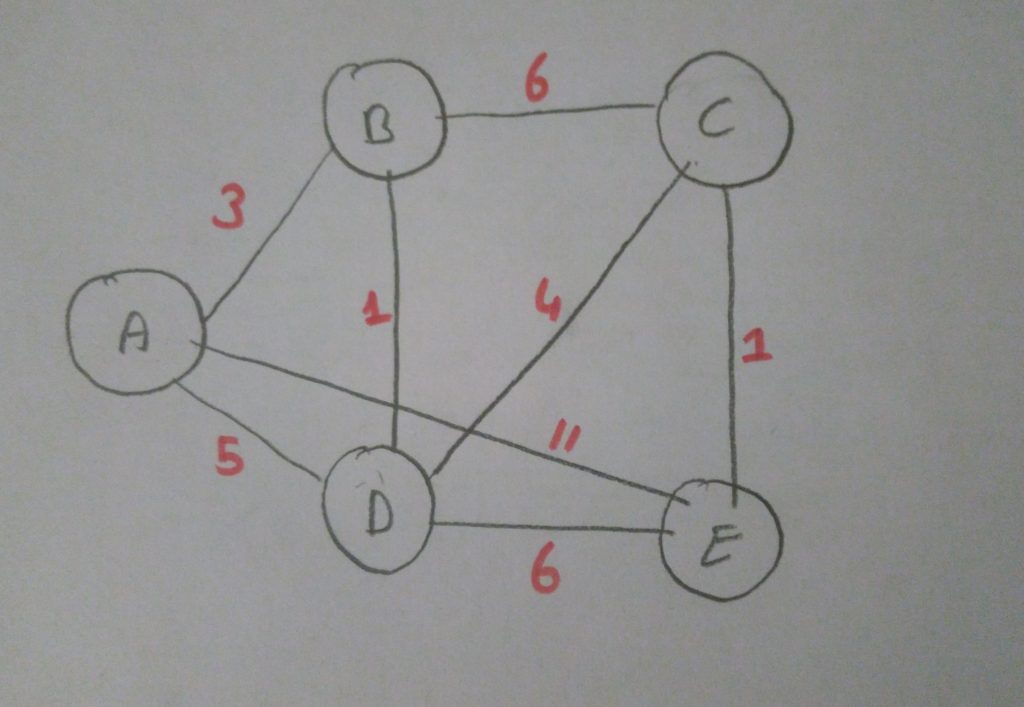
Grafımız bu şekilde olsun.
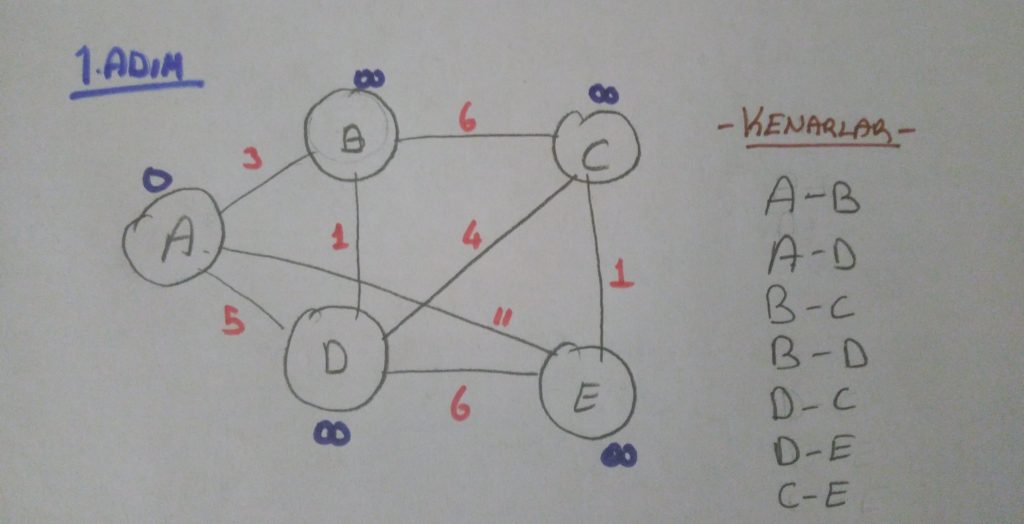
İlk adımda A değerine 0(sıfır) diğer düğümlere sonsuz değerini atıyoruz ve graf üzerindeki tüm kenarları bir kenara yazıyoruz.
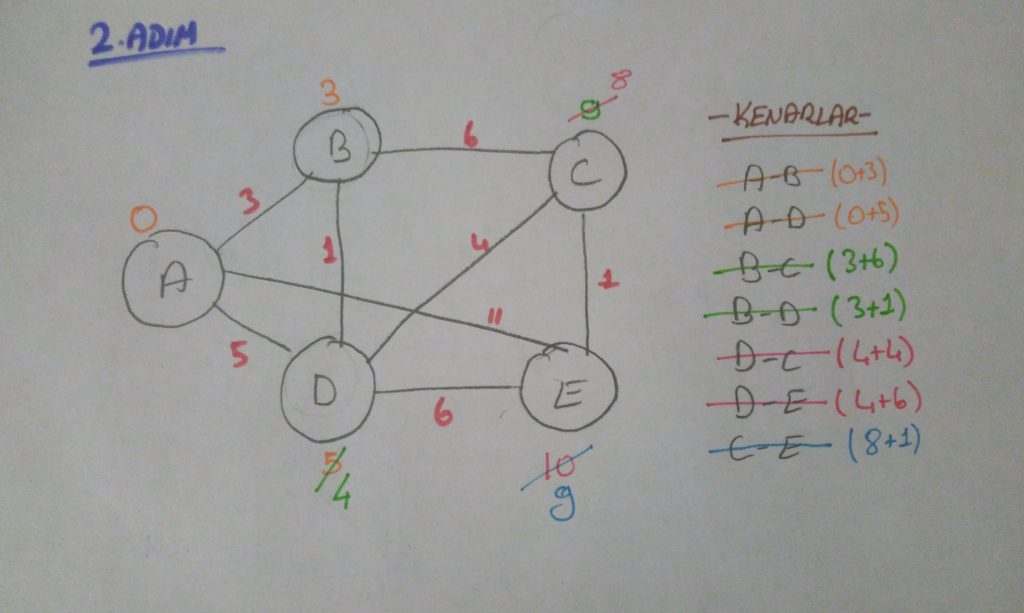
İkinci adımda Kenarlar üzerinde çizili olanlar turuncu renkten mavi renge doğru en güncel değerleri belirtir yani sırasıyla düğümler üzerine yazarsanız en güncel değeleri şekildeki gibi bulursunuz yani:
- A-0
- B-3
- C-8
- D-4
- E-9
şeklindedir.
Dijkstrayla bellman ford algoritmasının farkı
Bellman for algoritması eksi(-) değer taşıyan kenarlar üzerinde kullanılabiliyorken,dijkstra algoritması kullanılamaz.
Dijkstra algoritması,bellman ford algoritmasına göre hızlı çalışır.
Kısa yolu bulmada benzerlik gösterirler.
Eksi(-) değer taşıyan kenarlar ile ilgili örneği video üzerinde göstereceğim.