Graf,gerçek hayatta karşılaşılan birçok problemi,mantıksal ilişki kurarak problemi göstermeye yarayan bir ağ yapısıdır. Graf teorisi,çizge teorisi,çizge kuramı,grafları inceleyen bir matematik dalıdır.Bağlantılı listeler ve ağaçlar,grafların özel halidir.
Grafların kullanım alanları:
-
Fizik, kimya vb. temel bilim dallarında problemlerin veya konuların gösterilmesine yardımcı olur.
-
Ulaşımda otoyolların ve havayolların güzergahlarında kolaylık sağlar.
-
Elektrik ve elektronik mühendisliğinde,devreler üzerinde kullanılır.
-
Bilgisayar mühendisliği veya bilgisayar bilimlerinde(computer science) birçok alanda kullanılır.Bilgisayar ağları,dosya dizinleri,internet,veritabanı vs.
-
Bilgisayar oyunlarında kullanılır.
Görüldüğü gibi birçok farklı farklı alanlarda kullanılan graf teorisi (graph theory),hayatımızdaki problemleri basite indirgeyerek daha hızlı ve düzgün adımlar ile çözmemizi sağlar.
Graf teorisi (graph theory),1736 yılında Leonhard Euler tarafından “Königsberg’in yedi köprüsü” adlı matematik probleminin çözümüyle başlamıştır.
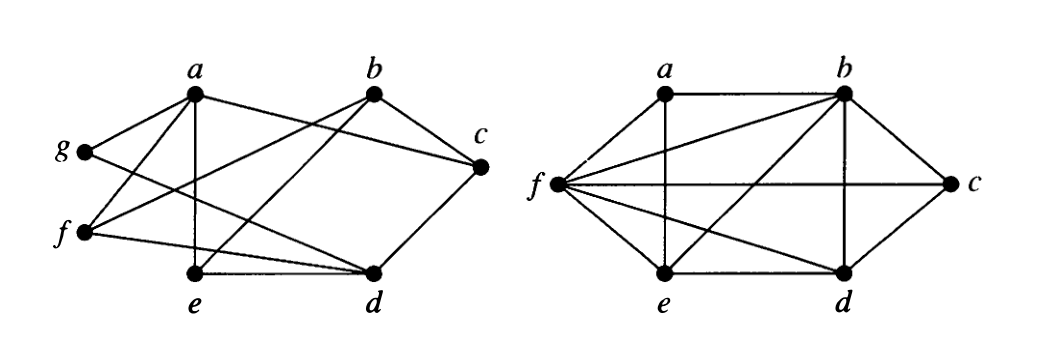
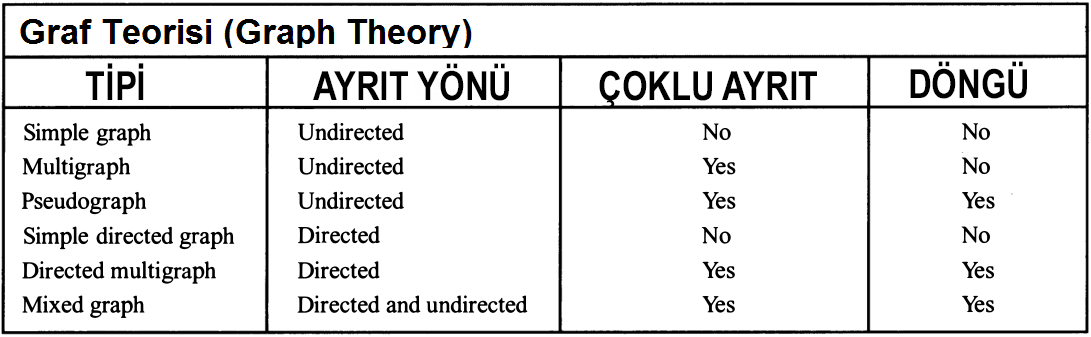
Yönsüz graf:G=(V,E) biçimde gösterilir.V(vertex) yani düğümler kümesidir ve boş olmayan kümedir.E(Edge) yani ayrıtlar kümesidir.Düğümlerin yönsüz ayrıtlarla bağlanmasındır.
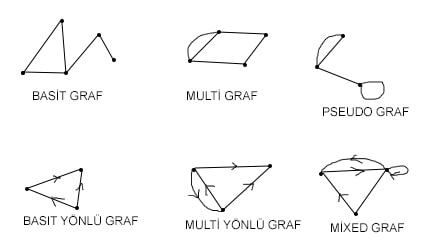
Basit graf:Bir grafta her ayrıt iki düğümü birleştirmişse(farklı düğümler) ve bu iki düğüm arasında birden fazla ayrıt yoksa buna basit graf denir.Döngü içermeyen graflardır.
Multi graf:Bir grafta aynı düğüm ikilisi arasında birden fazla ayrıt varsa buna multi graf denir.
Pseudo graf:Döngü(loop) ve multi graf içeren graflara pseudo graf denir.
Basit yönlü graf:Bir grafta,düğüm çiftleri arasında aynı yönlü sadece bir tane ayrıt varsa buna basit yönlü graf denir.
Multi(Çok) yönlü graf:Bir graftaki herhangi iki düğüm arasında birden fazla aynı yönlü graf varsa buna multi yönlü graf denir.
Mixed(Karışık) yönlü graf:Hem yönlü hem de yönsüz grafların olduğu graflardır.
Düğüm derecesi: Yönsüz grafta,bir düğüme bağlı olan ayrıt sayıdır. Deg(v) şeklinde gösterilir.
Yönsüz grafta döngü,düğümün derecesini 2 arttırır.
Derecesi 0 olan düğümlere izole düğüm,derecesi 1 olan düğümlerede uç düğüm ya da pendant denir.
Bazı özel graflar
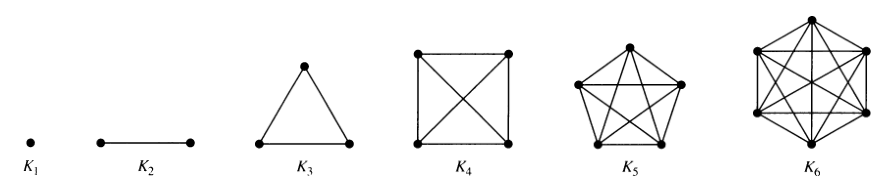
Tam(Complete) Graf
Kn ile gösterilir ve n düğüm sayısını ifade eder.Her bir düğüm çifti arasında tam olarak 1 tane ayrıt bulunan basit bir graftır.
İki kümeli graf(Bipartite graph)
Düğümler öyle bir iki kümeye ayrılmalıdır ki bir kenar ile birbirine bağlanabilecek durumda olan düğümleri aynı kümeye yerleştirilmemelidir. Yani mevcut küme içerisinde düğümler birbirine herhangi bir kenar ile bağlanmamalıdır. Teorem:Basit bir grafın bipartite olabilmesi için düğümler iki farklı renk ile boyandığında komşu düğümler aynı renk değilse bu graf bipartitedir.
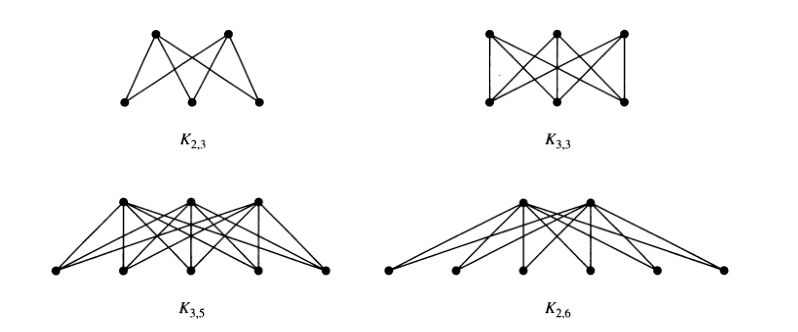
Tam iki kümeli graf(Complete bipartite graph)
Km,n şeklinde gösterirlir.Bir kümedeki her düğümden başka bir kümedeki düğümlerin her birine ayrıt varsa bu graf tam iki kümeli graftır.