Merge Sort Algoritması (Birleştirme Sıralaması) Verilerimizi sıralı hale getirmek için kulladığımız Merge Sort Algoritması(Birleştirme Sıralaması), parçala ve fethet(divide and conquer) yöntemiyle çalışır.
Çalışma Mantığı
Diziyi sürekli ikiye bölüp ve en küçük yani bölünemeyecek elemana sahip olana kadar devam eder. Daha sonra parçaladığı bu elemanları kendi içlerinde sıralayarak tıpkı bölerken uygulanan adımlar gibi bu sefer birleştirerek sıralayarak üst dizine geçer** ve birleştirme sonunda sıralı bir diziye ulaşılır.
Algoritması Adımları
Adım 1(Böl)
Verilen diziyi eşit bir şekilde iki alt diziye ayır.Ayırma işlemini alt dizinin iki elamnı olana kadar devam ettir.
Adım 2 (Yönet)
Alt dizinleri kendi aralarında sırala.
Adım 3 (Birleştir)
Sıralı dizinleri tek bir sıralı dizi oluncaya kadar birleştir.
Görüldüğü gibi divide and conquer(parçala ve fethet) yaklaşımı, recursive yani özyineli bir yapıdadır.Herhangi bir dilde yazacağız merge sort kodunu recursive şeklinde yazmanız gerekmektedir.
Merge Sort Örneği
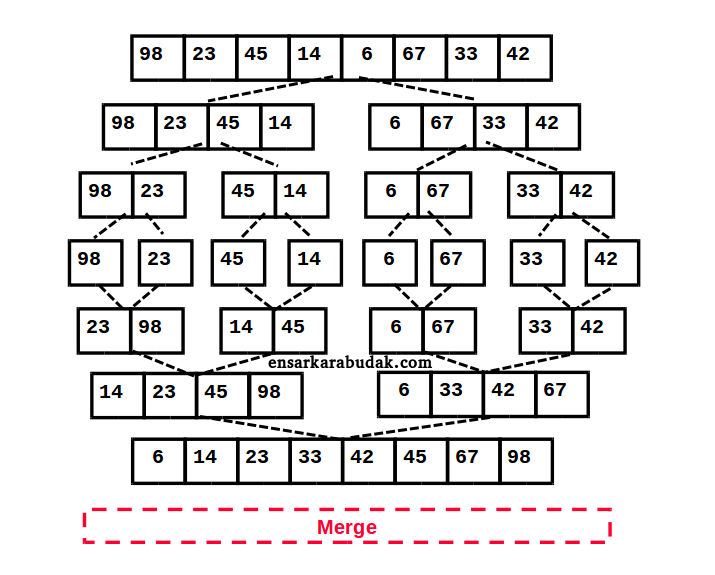
Not:Bölme aşamasında illa ikiye böleceğiz şekilde bir kural yoktur yani dizinizi üç,dört gibi eşit parçalarak bölebilirsiniz fakat bilgisayar bilimlerinde ikiye bölmek genel kabul edilmiş bir kuraldır.
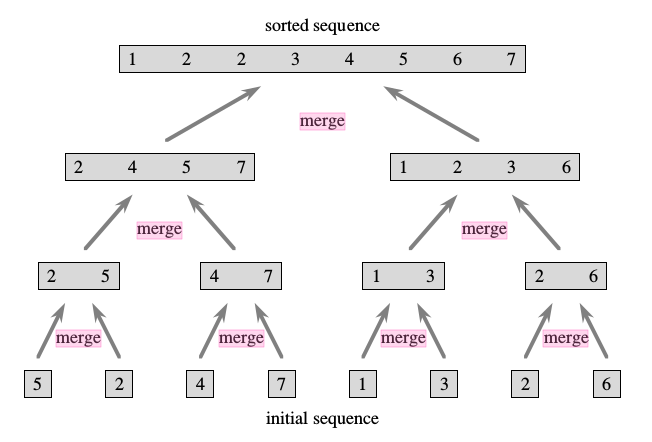
Merge(birleştirme) işleminin gerçekleştirimi
Merge Sort Algoritmasının Karmaşıklığı
Birleştirme sıralamasının karmaşıklığını hesaplamak için sıralanacak N elemanlı diziyi ağaç(tree) yapısına uygun bir şekilde taşıyınca ağaçtaki her bir düğüm bir alt diziyi temsil eder. Ağaç n tane seviye içerir.Buradaki n değeri değişkendir.K sayısı da 0’dan n-1’e kadar ağaç seviyesini temsil etsin. Yani ağaçta k.seviyede 2^n tane düğüm mevcuttur.
Bu düğümlerin her biri 2^{n-k}uzunluğunda bir alt diziyi belirtir.Yapılabilecek en fazla işlem sayısı ise 2^{n-k} olur.
N seviyesindeki bir ağaç için toplam n2^n karşılaştırma yapılır demektir. Elde edilen n2^n değerinin asimptotik üst sınırı O(nlogn) değeridir.
Bu özyinelemeli (recursive) bir yöntem olduğu için hep kendini çağırarak hep diziyi ikiye bölüyor. Böylelikle en fazla log2(N) kere bölme işlemi yapılmış oluyor. Her bölünmüş dizinin birleştirme işlemi içinde dizinin uzunluğu olan N işlem yapıldığı için bu algoritmanın karmaşıklık maliyeti büyük O notasyonunda(Big O) O(N*log(N))olur.
Sıralama algoritmaları arasında oldukça verimli olan Merge sort sayesinde çok kısa sürede büyük uzunluğundaki dizileri bile sıralıyabilir.
Merge Sort Java Kodu
Not: Kodu sizin yazıp öğrenmeniz amacıyla resim şeklinde verdim :)

Kod kaynak: erencetinkayaceng